第一章 单元测试
1、 问题:【问答题】
教育统计学、数理统计学和应用统计学具有怎样的关系?
正确答案:【
统计学按作用不同可分为两类:数理统计学和应用统计学。(1分)
1.应用统计学是按照应用的领域不同而划分的统计学,如,在医学领域应用的称为医学统计学,在经济领域应用的统计学称为经济统计学,在教育领域应用的统计学称为教育统计学;(1分)
2、而数理统计学是为各门应用统计学提供数理方法的一门学科,其内容主要是运用概率的知识来解释统计数据数量关系的模式,是数学的一大分支。(1分)
】
2、 问题:【问答题】
统计量和参数有何区别,请举出几个常见统计量和参数的表示符号。
正确答案:【
统计学中把总体的指标统称为参数.而由样本算得的相应的总体指标称为统计量.
(2分)
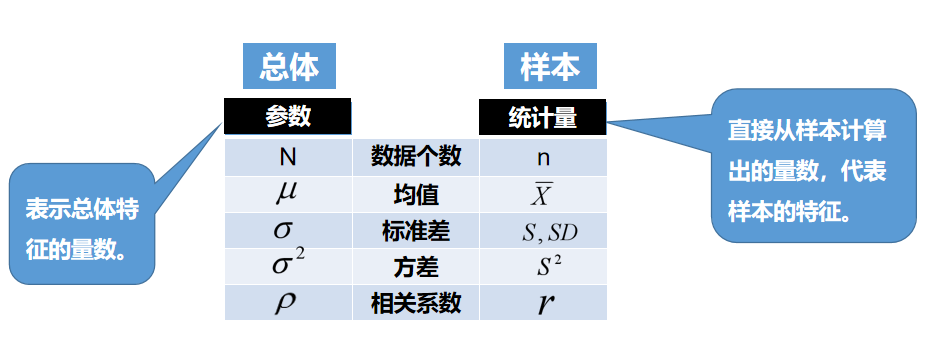
(2分)
】
3、 问题:【问答题】
SPSS中常用的变量包括定距型变量、定类型变量和定序型变量,请分别举例说明。
正确答案:【
1.定类数据(Nominal):名义级数据,数据的最低级,表示个体在属性上的特征或类别上的不同变量,仅仅是一种标志,没有序次关系。例如, ”性别“,”男“编码为1,”女“编码为2。(2分)
2.定序数据(Ordinal):数据的中间级,用数字表示个体在某个有序状态中所处的位置,不能做四则运算。例如,“受教育程度”,文盲半文盲=1,小学=2,初中=3,高中=4,大学=5,硕士研究生=6,博士及其以上=7。(2分)
3.定距数据(Interval):具有间距特征的变量,有单位,没有绝对零点,可以做加减运算,不能做乘除运算。例如,温度。(2分)
】
4、 问题:【问答题】
为研究山东省地方本科院校大学生的就业情况,某研究团队从山东省地方本科院校已经毕业五年的毕业生中,抽取了1500名毕业生进行调查研究,请你说出本研究的总体、个体和样本,并说明应如何科学地抽样这一样本?
正确答案:【
1.总体:山东省地方本科院校毕业五年的学生。(1分)
2.个体:山东省地方本科院校毕业五年的每一个大学生。(1分)
3.样本:从山东省地方本科院校中抽取的1500个毕业五年的大学生。(1分)
4.为保证样本抽取的科学性,可从山东省不同地区的本科院校抽取样本,并且考虑到不同的专业类别,如文科、理科和工科,以更细致地进行就业情况的分析。(2分)
】
5、 问题:
教育统计学的主要内容包括描述统计、推断统计和研究设计。
A:对
B:错
正确答案:【对】
第二章 单元测试
1、 问题:【问答题】
调查研究的基本过程包括哪几个环节?调查研究中,研究题目、研究目的和研究内容具有怎样的关系?
正确答案:【
研究目的决定研究内容(2分),
研究内容根据研究目的确定(2分),
同一个调查题目,由于目的不同,研究的内容也可能不同。
】
2、 问题:【问答题】
如何设计调查问卷。
正确答案:【
先确定调查的目的,再根据目的拟定主题,再确定较详细的内容(2分),
最后根据内容设计每部分的题目(2分)。
】
3、 问题:【问答题】
选择你感兴趣的主题,进行调查,写出调查的策划书并设计问卷。
正确答案:【
1.调查主题和目标。(3分)
2.调查的内容。(3分)
3.调查问卷,根据调查的内容设计问卷。(4分)
】
4、 问题:【问答题】
获得调查问卷的数据后,如何将其输入到SPSS软件中?
正确答案:【
分两步:
首先将每一个题目作为一个变量在SPSS中定义变量,并对每个题目的不同选项设定为某个固定的值;
然后再在数据视图中录入数据。
】
5、 问题:
SPSS中,“编码”和“计算变量”等功能会根据设置的要求修改原来的数据。
A:对
B:错
正确答案:【错】
第三章 单元测试
1、 问题:【问答题】
用自己的话解释以下概念:加权平均数、众数、中位数、方差、标准差。
正确答案:【
1.加权平均数:是指一组数据中每一个数据乘以它的权重所得之和;(1分)
2.众数:在一组数据中出现次数最多的数众数:在一组数据中出现次数最多的数叫做这组数据的众数;(1分)
3.中位数:把一组数据按从小到大的顺序排列,在中间的一个数字(或两个数字的平均值)叫做这组数据的中位数;(1分)
4.方差: 一般地,各数据与平均数的差的平方的平均数叫做这组数据的方差;(1分)
5.标准差:方差的算术平方根叫做标准差。(1分)
】
2、 问题:【问答题】
什么是3σ原则?
正确答案:【
在正态分布中σ代表标准差,μ代表均值x=μ即为图像的对称轴,三σ原则即为:
1.数值分布在(μ—σ,μ+σ)中的概率为0.6826;(1分)
2.数值分布在(μ—2σ,μ+2σ)中的概率为0.9544;(1分)
3.数值分布在(μ—3σ,μ+3σ)中的概率为0.9974;(1分)
可以认为,Y 的取值几乎全部集中在(μ—3σ,μ+3σ)]区间
内,超出这个范围的可能性仅占不到0.3%.
】
3、 问题:【问答题】
在一堂统计课上,教师进行了三项测试。每位学生的成绩都在原始成绩上有权重。测试一、测试二和测试三的权重分别是1、2和2。下面是一位学生的测试分数,求这个学生分数的总体平均数。
| 测试 | 1 | 2 | 3 |
| 分数 | 83 | 97 | 92 |
正确答案:【
92.2
】
4、 问题:
标准差与原始分数的量纲相同,因此,在表示数据的离散程度方向,标准差比方差更好理解。
A:对
B:错
正确答案:【对】
5、 问题:
在期末通考中,八年级一班英语平均成绩是85分,方差是36,张萌计算后得到的标准分数是-2分,求她得的原始分是多少?
A:97
B:76
C:80
D:71
正确答案:【76】
6、 问题:【问答题】
集中量数和差异量数各表示数据的什么特征?
正确答案:【
集中量数(集中趋势),反映频数分布中大量数据向一点集中的情况(1分)。差异量数表示各数据差异的程度(1分)。
】
第四章 单元测试
1、 问题:【问答题】
什么是抽样分布?它与样本分布和总体分布有什么区别?
正确答案:【
1.抽样分布是指某种样本统计量的分布,即把某种样本统计量看作一个随机变量,这个随机变量的全部值构成的新的总体所形成的分布即为该种统计量的抽样分布。(2分)
2.如一项研究,需要了解某市初一学生的体重。从全市学生中随机抽取50人构成一个样本,这50人的体重就构成了一个样本分布;对于每一个样本,都可以求出一个样本均值,每个样本均值作为一个个体,抽取的所有样本求得均值,就构成一个均值的抽样分布。(3分)
】
2、 问题:【问答题】
中心极限定理的内容是什么?举例说明。
正确答案:【
用极限的方法求随机变量分布的一系列定理,其内容为:
(1)中心极限定理指的是给定一个任意分布的总体。每次从这些总体中随机抽取 n 个个体,一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布。(抽样分布与基本数据分布模型的关系)(1分)
(2)从总体抽取容量为n的一切可能样本时,所有样本均数的均数等于总体均数。(抽样分布与基本数据分布的均数关系)(1分)
(3)从总体抽取容量为n的一切可能样本时,所有样本均数的标准差等于总体标准差除以样本容量的算术平方根。(抽样分布的标准误和基本数据分布的标准差的关系)(1分)
举例(略)(2分)
】
3、 问题:【问答题】
以平均数为例,正态分布(或渐近正态分布)中,检验值与样本均数、总体均数以及标准误有何关系?
正确答案:【
由公式Z=(样本均数–总体均数)/标准误 可知,Z值与样本均数和总体均数的差成正比,与标准误成反比。(3分)
】
4、 问题:【问答题】
什么是t分布,它的标准误和检验值如何理解?如何计算?
正确答案:【
σ2未知,n<30时,样本均数和样本标准差的分布不再是正态分布。统计学家高赛特(Gosset)提出了一种由小样本统计量形成的概率分布,称为t分布。 (2分)
标准误是指对应抽样分布,一个样本均值距离总体均值的离散程度,它反映了这个样本均值代表总体均值的情况,它的值越小,说明距离总体均值越近。(2分)
t检验值等于样本均值减总体均值除以标准误。
检验值是指根据t值的计算公式,由样本数据求得的一个检验值,利用t分布表,可查出t值对应的概率p,再比较p值大小和显著性水平,从而判定是否拒绝原假设。(2分)
】
5、 问题:【问答题】
举例说明如何查t分布表?
正确答案:【
如,某市小学五年级数学竞赛平均成绩为67分,某校参加17人,平均成绩为72分,标准差Sn = 10分,问该校成绩是否高于全市平均成绩?
由公式求得72分对应的t值为2(1分);
取显著性水平α=0.05,知自由度df=17-1=16。查t分布表,自由度为16和显著性水平α =0.05的交界处即为单侧临界值:t0.05(16)=1.746;(1分)
由于t=2>1.746, p<0. 05,所以拒绝原假设,认为该校成绩高于全市的平均成绩。(1分)
】
6、 问题:【问答题】
判断下列问题是双边检验还是单边检验,并建立零假设和备择假设。
(1)某学校想检验本单位职工每学期的请教次数是否不超过3次。
(2)某市通考中,全市五年级数学平均成绩为80分,预检验某校的平均分是否跟全市的平均分有显著差异。
(3)某班每月学生上学迟到的平均次数是4次,该班为加强管理,准备实施一项有效的班级管理制度,以减少迟到现象,试检验这一制度实施的有效性。
(4)学校初一1班和2班要比较两个班的期末成绩是否显著不同。
(5)初二年级有8个班,他们进行了一次数学考试,检验各班级的平均分数有无显著差异。
正确答案:【
(1)单侧检验:
H0:本单位职工每学期的请教次数不超过3次。
H1:本单位职工每学期的请教次数超过3次。(2分)
(2)双侧检验:
H0:某校的平均分跟全市的平均分无显著差异。
H1:某校的平均分跟全市的平均分有显著差异。(2分)
(3)双侧检验:
H0:班级管理制度以减少迟到现象无显著差异。
H1:班级管理制度以减少迟到现象有显著差异。(2分)
(4)双侧检验:
H0:初一1班和2班要比较两个班的期末成绩无显著不同。
H1:初一1班和2班要比较两个班的期末成绩显著不同。(2分)
(5)双侧检验:
H0:各班级平均分无显著不同。
H1:各班级平均分有显著不同。(2分)
】
7、 问题:【问答题】
统计假设检验中的p值是什么?怎样根据p值进行假设检验?
正确答案:【
1.P值是对应于检验值(如t值)计算出来的概率值,当p值小于显著性水平0.05或0.01时,即零假设被拒绝,接收备择假设;(2分)
2.当p值大于显著性水平0.05或0.01时,即零假设被接受;比较p值与显著性水平的方法与比较检验值(如t值)与临界值的方法是相同的。(2分)
】
8、 问题:【问答题】
结合正态分布或t分布图,明确显著性水平、临界值、拒绝域和接受域、t值、P值的关系,并举例说明假设检验的基本思想。
正确答案:【
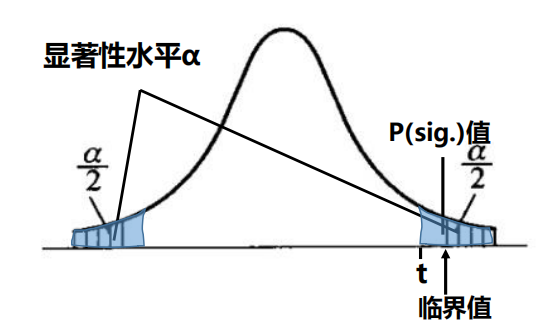
1.显著性水平是给定的一个可能性的概率,它是指在多大程度上具有拒绝的可能,它一般取0.05或0.01;(1分)
2.t值是根据样本数据算出来的一个统计量的值,临界值是指一个拒绝零假设的界限值,当t值大于临界值时,就会拒绝零假设;(1分)
3.P值是对应于t值计算出来的概率值,当p值小于显著性水平0.05或0.01时,即零假设被拒绝; (1分)
举例(图)(1分)
】
9、 问题:【问答题】
区别以下概念
(1)双侧检验和单侧检验 (3)拒绝域和接受域、
正确答案:【
(1)双侧检验和单侧检验(2分)
问题的提法不同,双侧检验研究的是新方法与旧方法是否有差异;单侧检验研究的是新方法明显好于旧方法还是新方法明显不如旧方法;
建立假设的形式不同,双侧检验的假设是 H0: u=u0 H1: u ≠u0;单侧检验的假设是 H0: u≤u0 H1: u>u0 或 H0: u<u0 H1: u≤u0;
否定的区域不同,双侧检验的否定区域是 |Z|> Z a/2;单侧检验的否定区域是 Z<-Za 或 Z>Za
(2)拒绝域和接受域(2分)
在假设检验中,据以拒绝原假设的统计量的取值范围,假设检验中根据检验统计量的分布,由给定的小概率α(0<α<1)作为显著性水平所确定的拒绝原假设H0的区间称为拒绝域,即统计量在其中取值的概率为α的区域。它是能够拒绝原假设的检验统计量的所有可能取值的集合;
不能够拒绝原假设的检验统计量的所有可能取值的集合称为接受域;根据给定的显著性水平确定的拒绝域的边界值,称为临界值。
】
10、 问题:【问答题】
统计推断中,用样本推断总体的条件是什么?
正确答案:【
样本随机性(1分),能够代表总体。(1分)
】
11、 问题:【问答题】
什么是单样本t检验,它的条件是什么?
正确答案:【
1.单样本t检验是用來确定样本均值 (x) 是否与已知或假设的总体均值 (µ) 在统计上有显著的不同。单样本t检验是一种参数检验。(2分)
2.条件:已知总体均数;单变量为计量资料且符合正态分布。(2分)
如有任何疑问请及时联系QQ 50895809